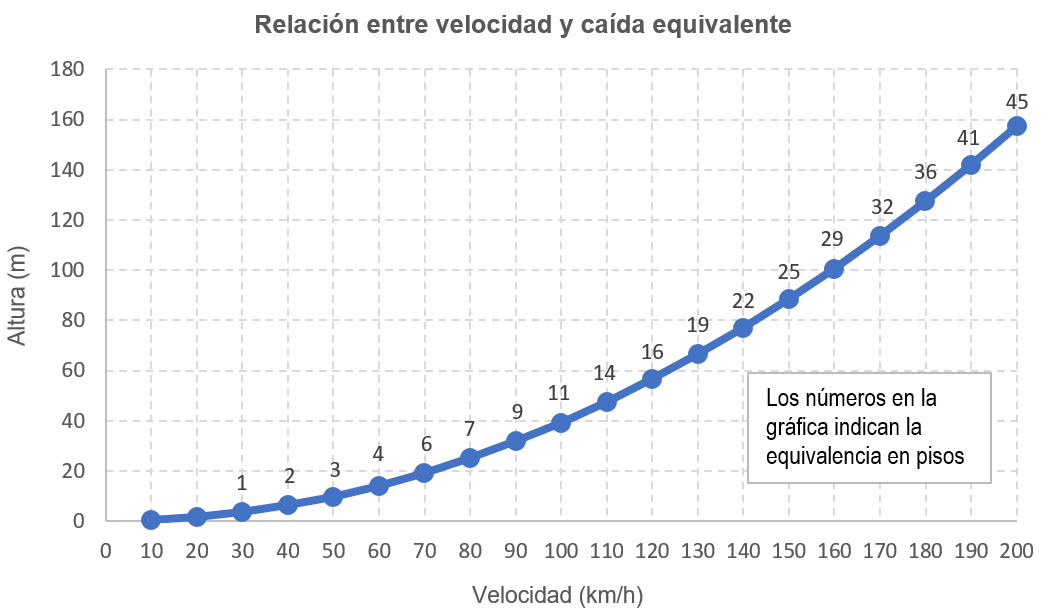
La Dirección General de Tráfico recurre frecuentemente a la equivalencia entre velocidad y caída desde una altura determinada para ayudarnos a ser conscientes de la severidad que puede tener una colisión. Sin embargo, la Institución no explica cómo obtiene esa equivalencia, por lo que es interesante disponer de algún sencillo método de cálculo que nos permita hacer nuestras propias estimaciones.
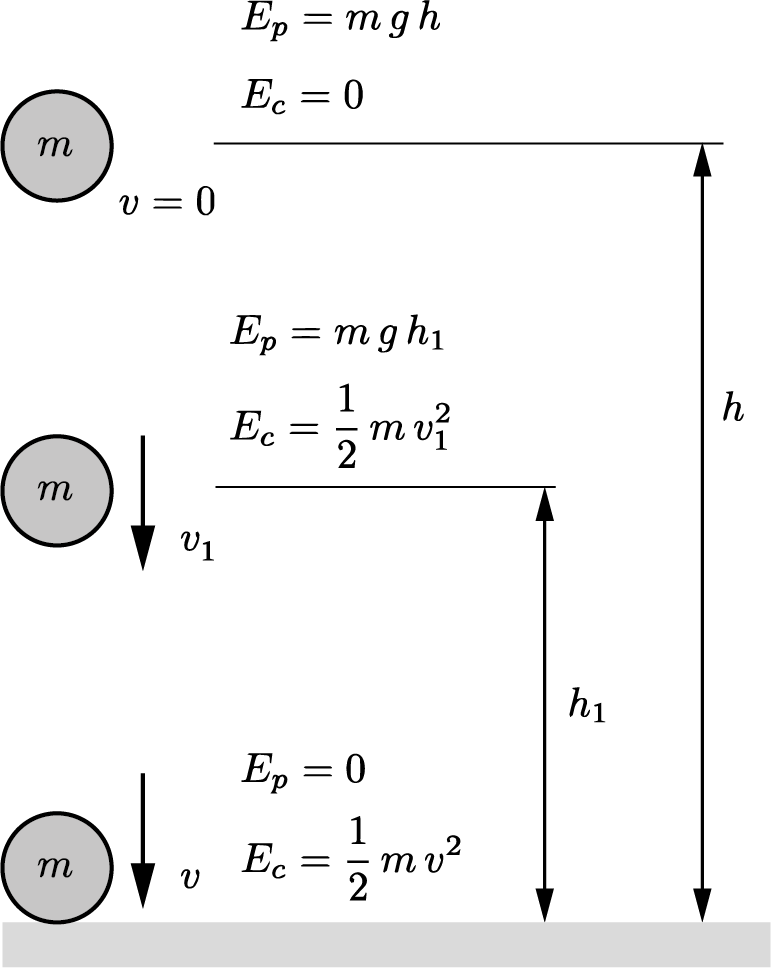Este método de cálculo lo deduciremos a partir del principio de la conservación de la energía que aplicaremos al caso concreto de una bola de masa \( m \) que cae libremente desde una altura \( h \)., tal como muestra el esquema.
Durante la caída y en todo momento, la bola poseerá dos tipos de energía: potencial y cinética.
- La energía potencial, \( E_p \), dependerá de la altura a la que se encuentre la bola y vendrá dada por:
$$ E_p = m \, g \, h $$
- La energía cinética, \( E_c \), dependerá de la velocidad con la que se mueva la bola y vendrá dada por:
$$ E_c = \frac{1}{2} \, m \, v^2 $$
Aplicando el principio de conservación de la energía, sabemos que en cualquier instante de la caída la energía mecánica total, \( E_m \), obtenida como suma de energía potencial más energía cinética, valdrá siempre lo mismo.
$$ E_m = E_p + E_c = \text{Constante} $$
Consideraremos ahora tres instantes de la caída de la bola:
- En el instante inicial, la bola está detenida, por lo que su energía cinética es nula y solo posee energía potencial. Por tanto:
$$ E_m = E_p + 0 = m \, g \, h $$
- En un punto intermedio de la caída, a una altura \( h_1 \) del suelo, moviéndose la bola con ujna velocidad \( v_1 \), ésta poseerá tanto energí potencial como energía cinética:
$$ E_m = E_p + E_c = m \, g \, h_1 + \frac{1}{2} \, m \, v_1^2 $$
- En el instante final, cuando la bola llegue al suelo, moviéndose con ujna velocidad \( v \), ésta no poseerá energía potencial, pero sí energía cinética:
$$ E_m = 0 + E_c = \frac{1}{2} \, m \, v^2 $$
Por tanto, en los tres instantes que hemos considerado, se tiene que verificar que:
$$ E_m = m \, g \, h = m \, g \, h_1 + \frac{1}{2} \, m \, v_1^2 = \frac{1}{2} \, m \, v^2 $$
Tomando los instantes inicial y final podemos ya relacionar la altura desde la que cae la bola con su velocidad al llegar al suelo.
$$ m \, g \, h = \frac{1}{2} \, m \, v^2 \Rightarrow h = \frac{v^2}{2 \, g} $$
En esta expresión, la velocidad debe ser introducida en m/s, obteniéndose la altura expresada en metros. Si deseamos estimar la altura de caída introduciendo la velocidad en km/h, basta con introducir el factor de cambio de unidades:
$$ h = \frac{v^2}{3,6^2 \left( 2 \, g \right)} $$
En la gráfica se muestra la relación entre altura de caída y velocidad hasta 200 km/h, así como la equivalencia en pisos (suponiendo cada piso de 3,5 metros de altura).
